Her Programcının Bilmesi Gereken 6 Veri Yapısı

Yetkin ve başarılı bir programcı olmanın yolu zordur, ancak kesinlikle ulaşılabilirdir. Veri yapıları, her programlama öğrencisinin ustalaşması gereken temel bir bileşendir ve muhtemelen diziler veya listeler gibi bazı temel veri yapılarını öğrenmiş veya bunlarla çalışmış olabilirsiniz.

Görüşmeciler, veri yapıları ile ilgili sorular sormayı tercih etme eğilimindedir, bu nedenle bir iş görüşmesine hazırlanıyorsanız, veri yapıları bilginizi tazelemeniz gerekecektir. Programcılar ve iş görüşmeleri için en önemli veri yapılarını sıralarken okumaya devam edin.

Bağlantılı listeler, en temel veri yapılarından biridir ve çoğu veri yapısı dersinde öğrenciler için genellikle başlangıç ​​noktasıdır. Bağlantılı listeler, sıralı veri erişimine izin veren doğrusal veri yapılarıdır.

Bağlantılı listedeki öğeler, işaretçiler kullanılarak bağlanan (bağlı) ayrı düğümlerde depolanır. Bağlantılı bir listeyi, farklı işaretçiler aracılığıyla birbirine bağlı bir düğümler zinciri olarak düşünebilirsiniz.

İlişkili: Java'da Bağlantılı Listeleri Kullanmaya Giriş

Farklı bağlantılı liste türlerinin özelliklerine girmeden önce, bireysel düğümün yapısını ve uygulamasını anlamak çok önemlidir. Bağlantılı listedeki her düğüm, onu listedeki bir sonraki düğüme ve veri öğesinin kendisine bağlayan en az bir işaretçiye sahiptir (çift bağlantılı liste düğümlerinin iki işaretçisi vardır).

Her bağlantılı listenin bir baş ve kuyruk düğümü vardır. Tek bağlantılı liste düğümleri, zincirdeki bir sonraki düğüme işaret eden yalnızca bir işaretçiye sahiptir. Bir sonraki işaretçiye ek olarak, çift bağlantılı liste düğümleri, zincirdeki bir önceki düğüme işaret eden başka bir işaretçiye sahiptir.

Bağlantılı listelerle ilgili görüşme soruları genellikle belirli bir öğenin eklenmesi, aranması veya silinmesi etrafında döner. Bağlantılı bir listeye ekleme O(1) zaman alır, ancak en kötü durumda silme ve arama O(n) zaman alabilir. Dolayısıyla bağlantılı listeler ideal değildir.

2. İkili ağaç

İkili ağaçlar, ağaç ailesi veri yapısının en popüler alt kümesidir; bir ikili ağaçtaki öğeler bir hiyerarşi içinde düzenlenir. Diğer ağaç türleri arasında AVL, kırmızı-siyah, B ağaçları vb. bulunur. İkili ağacın düğümleri, veri öğesini ve her alt düğüme iki işaretçi içerir.

İkili bir ağaçtaki her bir üst düğüm en fazla iki alt düğüme sahip olabilir ve her bir alt düğüm sırayla iki düğümün ebeveyni olabilir.

İlişkili: İkili Ağaçlara Yeni Başlayanlar İçin Kılavuz

İkili arama ağacı (BST), verileri ana değerden daha küçük bir anahtar/değere sahip öğelerin bulunduğu sıralı bir düzende depolar. düğüm solda depolanır ve ana düğümden daha büyük bir anahtar/değere sahip öğeler, sağ.

İkili ağaçlara genellikle röportajlarda sorulur, bu nedenle bir röportaja hazırlanıyorsanız ikili bir ağacı nasıl düzleştireceğinizi, belirli bir öğeyi nasıl arayacağınızı ve daha fazlasını bilmelisiniz.

3. Hash Tablosu

Karma tablolar veya karma haritalar, verileri bir dizi biçiminde depolayan oldukça verimli bir veri yapısıdır. Her veri öğesine, verimli arama ve silme işlemine izin veren bir karma tablosunda benzersiz bir dizin değeri atanır.

Bir hash haritasında anahtar atama veya eşleme işlemine hashing denir. Hash fonksiyonu ne kadar verimli olursa, hash tablosunun kendisinin verimliliği o kadar iyi olur.

Her karma tablo, veri öğelerini bir değer-endeks çiftinde saklar.

Burada değer, depolanacak veridir ve dizin, öğeyi tabloya eşlemek için kullanılan benzersiz tam sayıdır. Hash fonksiyonları, hash tablosunun gerekli verimliliğine ve çarpışmaları nasıl çözeceğinize bağlı olarak çok karmaşık veya çok basit olabilir.

Çarpışmalar genellikle, bir karma işlevi farklı öğeler için aynı eşlemeyi ürettiğinde ortaya çıkar; karma harita çakışmaları, açık adresleme veya zincirleme kullanılarak farklı şekillerde çözülebilir.

Karma tabloları veya karma haritaları, kriptografi dahil olmak üzere çeşitli farklı uygulamalara sahiptir. Sabit O(1) zamanında ekleme veya arama gerektiğinde ilk tercih edilen veri yapısıdır.

4. Yığınlar

Yığınlar, daha basit veri yapılarından biridir ve ustalaşması oldukça kolaydır. Bir yığın veri yapısı, esasen herhangi bir gerçek yaşam yığınıdır (bir kutu veya plaka yığınını düşünün) ve bir LIFO (Son Giren İlk Çıkar) tarzında çalışır.

Yığınların LIFO özelliği, en son eklediğiniz öğeye önce erişileceği anlamına gelir. Bir yığındaki üst öğenin altındaki öğelere, üstündeki öğeleri açmadan erişemezsiniz.

Yığınların iki temel işlemi vardır: itme ve patlatma. Push, yığına bir öğe eklemek için kullanılır ve pop, en üstteki öğeyi yığından kaldırır.

Ayrıca çok sayıda faydalı uygulamaları vardır, bu nedenle görüşmecilerin yığınlarla ilgili sorular sorması çok yaygındır. Bir yığını nasıl tersine çevireceğinizi ve ifadeleri nasıl değerlendireceğinizi bilmek oldukça önemlidir.

5. Kuyruklar

Kuyruklar yığınlara benzer ancak FIFO (İlk Giren İlk Çıkar) tarzında çalışır, yani daha önce eklediğiniz öğelere erişebilirsiniz. Kuyruk veri yapısı, insanların geliş sırasına göre konumlandığı herhangi bir gerçek hayattaki kuyruk olarak görselleştirilebilir.

Bir kuyruğa ekleme işlemine kuyruğa alma denir ve bir elemanın kuyruğun başlangıcından silinmesine/kaldırılmasına kuyruğa alma denir.

İlişkili: Kuyrukları ve Öncelikli Kuyrukları Anlamak için Başlangıç ​​Kılavuzu

Öncelik sıraları, CPU zamanlaması gibi birçok hayati uygulamada sıraların ayrılmaz bir uygulamasıdır. Öncelik kuyruğunda, öğeler varış sırasına göre değil, önceliklerine göre sıralanır.

6. yığınlar

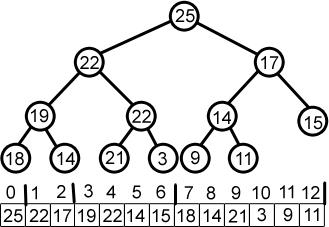
Yığınlar, düğümlerin artan veya azalan düzende düzenlendiği bir tür ikili ağaçtır. Bir Min Yığında, ebeveynin anahtar değeri, alt öğelerinin anahtar değerine eşit veya daha küçüktür ve kök düğüm, tüm yığının minimum değerini içerir.

Benzer şekilde, bir Maks Yığının kök düğümü, yığının maksimum anahtar değerini içerir; yığın boyunca min/maks yığın özelliğini korumanız gerekir.

İlişkili: Yığınlar vs. Yığınlar: Onları Ayıran Nedir?

Yığınlar, çok verimli yapıları nedeniyle birçok uygulamaya sahiptir; öncelikle, öncelik sıraları genellikle yığınlar aracılığıyla uygulanır. Ayrıca, yığın sıralama algoritmalarında temel bir bileşendir.

Veri Yapılarını Öğrenin

Veri yapıları ilk başta can sıkıcı görünebilir, ancak yeterince zaman ayırın ve bunları pasta kadar kolay bulacaksınız.

Bunlar programlamanın hayati bir parçasıdır ve hemen hemen her projede bunları kullanmanız gerekir. Belirli bir senaryo için hangi veri yapısının ideal olduğunu bilmek çok önemlidir.

Her Programcının Bilmesi Gereken 7 Algoritma

Bu algoritmalar, her programcının iş akışı için gereklidir.

Sonrakini Oku

Yazar hakkında